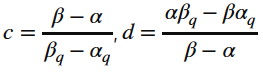Quantization
Mapping input values from a large set to output values in a smaller set신호 처리에서 Quantization은 어떤 입력 값(높은 해상도)을 더 작은 출력 값(낮은 해상도)으로 매핑하는 것을 의미한다.

위 예시를 보면, 0과 1 사이의 Signal이라고 가정, 파란색 선처럼 연속적인 값이 들어오면 빨간색 선처럼 Quantized 된 신호로 표현하고자 함.
여기서 빨간색 선은 4구간(-0.75, -0.25, 0.25, 0.75)으로 나뉘어져 있음. 구간 간격 0.5.
여기서 Quantization Error(Original-Quantized)는 최대 "구간 간격의 절반"이 됨
NN in Quantization
AlexNet을 iPhone에서 돌리고자 한다면 허용된 RAM의 크기에 비해 모델의 크기가 더 커서 어려움을 겪음
그런데, 학습된 가중치 분포를 찍어봤더니 대부분의 값이 -10~10 사이에 있었음.
Bit Encoding을 적용하고자 했고 여기서 NN in Quantization이 시작

위 그림은 Inception v3 모델의 첫번째 Conv layer의 가중치 분포이다.
값과 그래프를 살펴보면 대게 0 근처에 분포되어 있음
- 0 근처에서 촘촘하고, 대체로 0기준 대칭인 경향
- 2.0 이상의 값은 그리 많지 않음
- 대부분의 histogram slot은 비어있음

이에 기반하여 기존의 32bit float 값을 8bit int로 Fixed point mapping함.
-> 모델의 크기를 매우 작게 가져감, 연산 할때는 값을 다시 reconstruct해서 사용
quantized_code = uint8(((original - min) / (max - min)) * 255)
reconstructed = ((quantized_code / 255.0) * (max - min)) _ min
Quantization Error는 최대 "구간 간격의 절반"이기 때문에, 이 예제는 약 0.02의 값을 가짐
Quantization 이점
모델 사이즈를 줄여주는 것 이외의 이점

하드웨어에서는 MAC(Multiply-Accumulate) unit을 통하여 해당 연산을 수행

Quantization이 수행되면 FP32 타입이 Int8 타입으로 대치되기 때문에 이너지 소비 관점 이점이 있음

또한 모델의 크기가 줄어서 한번에 읽어오는 크기가 늘어나므로(x4 bandwidth), 더 효율이 좋아짐.
Fixed point

Fixed point는 등간격으로 수를 표현하는 방법이다. 그래서 항상 동일한 해상도를 가짐
Fixed point는 m개의 bit를 가지는 Signed Integer와 n개의 bit를 가지는 Fractional part로 구성
예를 들어, m=8, n=24인 경우
-128 ~ 127 : 정수 범위
1 / 2 ² ⁴ : Resolution
Floating point

Floating point는 Fixed point와 다르게 가변적으로 수를 표현함
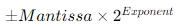
: 수의 표현
Floating point는 부호를 나타내는 1bit, m개의 bit를 가지는 exponent, n개의 bit를 가지는 Mantissa로 이루어져있음
-2 ¹ ² ⁶ ~ 2 ¹ ² ⁷ : 정수범위
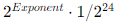
: Resolution

Bit가 주어졌을 때 Floating point를 계산해본다면 (위 수식에 값을 대입)
0.15625이라는 값이 나옴
Fixed point VS Floating point
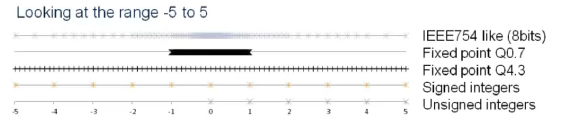
위 그림은 Fixed point 와 Floating point(IEEE754)의 차이점을 나타낸다.
Floating point는 가변간격이다.
Mantissa(가수부)와 Exponet(지수부)의 곱으로 수를 표현하기 때문에 Mantissa의 값에 따라서 구간이 더 넓어지거나 좁아질 수 있다.

Quantization mapping
Quantization Mapping
다음 두 과정 포함
- Quantization : High precision -> Low precision 변환
- De-Quantization : Low precision -> High precision 변환
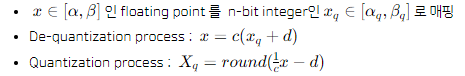
여기서 c와 d는 변수인데 각각 scale과 shift의 역할을 담당
구간( [α,β] )을 설정하고, 아래 조건을 만족하면 c와 d의 값을 구할 수가 있음
- 조건: x = α 일때, x_q =α_q 를, x = β 일때, x_q =β_q
그래서 위 선형시스템의 해는 다음이 됨.